TLmodel – Model for transmission line resonator¶

Module for the calculation of transmission line impedances

Most functions require a dictionary with specific elements regarding circuit parameters in it.:

params = {
    'Z0': 64.611, # characteristic impedance of TL resonator (e.g. geometric and kinetic), in Ohm
    'Cj': 1.77e-15, # Capacitance of the junction (RCSJ model) loading the TL resonator, in F
    'Z0p': 50, # reference impedance of the input line, in Ohm
    'Lg': 1.0432952403781536e-10, # geometric inductance of the junction leads loading the TL resonator, in H
    'Rj': 1027.6618763504205, # Resistance of the junction (RCSJ model) loading the TL resonator, in Ohm
    'n': 2.876042565429968, # refraction index for the TL resonator (v_ph = c / n)
    'type': 'lambda/2', # expected type of TL resonator. Only used in Zincircuit_approx. Can be 'lambda/2', 'lambda/4'
    'alpha': 0.0060728306929787035,  # attenuation constant for the TL resonator. This mainly sets the internal losses, in 1/m
    'Lj': 2.0916766016363636e-10, # Josephson inductance of the junction (RCSJ model) loading the TL resonator, in H
    'Pin': -122, # input power at the coupler of the TL resonator, in dBm
    'Cs': 2.657e-11, # shunt capacitance of the coupler, in F
    'l': 0.006119 # length of the TL resonator, in m
    }

The model calculated here is valid for a transmission line resonator coupled to the input line via a shunt capacitance Cs. At the far end, the TL resonator can be loaded by a RCSJ-type junction with an extra series inductor Lg and parallel capacitance Cg.

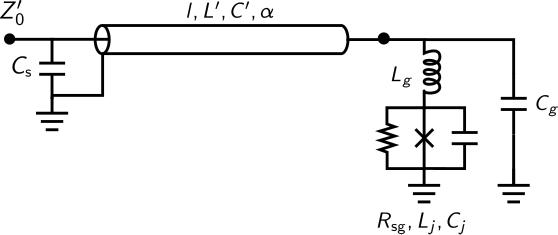
Circuit model used for TLmodel.py.¶

For more details see A ballistic graphene superconducting microwave circuit

Functions¶

stlabutils.TLmodel.FindParFromRes(params, w0, a, b, par='Lj', wws=None)[source]¶

Function to find value of a parameter to match a given resonance frequency

Finds approximate value of par to have an angular resonance frequency of w0. a,b is the bracketing interval. In our processing, the objective is to extract the load parameters from given resonance features, like the resonance frequency. Given w0, this function provides an initial estimate of these parameters to then perform the final fit such that the resonance frequency will start close to this value (for fit convergence).

Parameters

params (dict) – Dictionary containing model parameters
w0 (float) – Desired angular resonance frequency
a (float) – Bottom of bracketing interval for the parameter
b (float) – Top of bracketing interval for the parameter
par (str, optional) – Key of the parameter in params to be swept
wws (None or array, optional) – Angular frequency range to evaluate the circuit impedance at.

Returns

par0 – Parameter value that satisfies desired resonance frequency for the given parameters

Return type

float

stlabutils.TLmodel.Ij(omega, params)[source]¶

Total current going out the far end of the TL

Parameters

omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

Vl – Current phasor through the load

Return type

complex

stlabutils.TLmodel.Ix(x, omega, params)[source]¶

Current phasor at a given distance along the TL

Distance x counts from the load (at 0) to l (at input)

Parameters

x (float) – Position along the TL to calculate the current at, counting from the load (at 0) to l (at input)
omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

Current phasor at a given distance along the TL

Return type

complex

stlabutils.TLmodel.PintoV0(params)[source]¶

Conversion from power to voltage

Parameters: params (dict) – Dictionary containing model parameters
Returns: Incoming voltage amplitude for a given power
Return type: float

stlabutils.TLmodel.S11(Zin, params)[source]¶

Exact expression of S11 for a given input impedance and parameters

Parameters

Zin (complex or array of complex) – Load impedance
params (dict) – Dictionary containing model parameters

Returns

result – Values of S11 for the given input parameters

Return type

complex or array of complex

stlabutils.TLmodel.S11theo(f, f0, kint, kext)[source]¶

Lorentzian absortion function

Approximate formula for a Series RLC circuit capacitively coupled on one side to a transmission line. The frequencies can be either angular or ‘real’ ones, as long as all of them have the same type.

Parameters

f (float or array of float) – Frequency parameter
f0 (float) – Resonance frequency
kint (float) – Internal linewidth or loss rate
kext (float) – External linewidth or loss rate

Returns

Values of S11 for the given input parameters

Return type

float or array of float

stlabutils.TLmodel.Vin(omega, params)[source]¶

Voltage phasor at the input

If Pin is in params, it is used to calculate the actual amplitudes. If not, we assume an amplitude of 1V for the incoming wave.

Parameters

omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

result – Voltage phasor at the input

Return type

complex

stlabutils.TLmodel.Vj(omega, params)[source]¶

Voltage at the far end of the TL across a Josephson junction (RCSJ)

If there is a Lj and Cg in params, returns the voltage accross the junction (complex). Else, just the load voltage

Parameters

omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

Vl – Voltage phasor at the far end of the TL

Return type

complex

stlabutils.TLmodel.Vx(x, omega, params)[source]¶

Voltage phasor at a given distance along the TL

Distance x counts from the load (at 0) to l (at input)

Parameters

x (float) – Position along the TL to calculate the voltage at, counting from the load (at 0) to l (at input)
omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

result – Voltage phasor at a given distance along the TL

Return type

complex

stlabutils.TLmodel.ZTL(Z0, Zl, gammal)[source]¶

Impedance of a general terminated transmission line

Calculates the input impedance of a termniated transmission line with a given load impedance

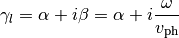
$\gamma_l = \alpha + i\beta = \alpha+i\frac{\omega}{v_{\rm ph}}$

Parameters

Z0 (complex) – line impedance
Zl (complex) – load impedance
gammal (complex) – propagation constant including losses

Returns

result – Impedance of the terminated TL

Return type

complex

stlabutils.TLmodel.Zcoup(omega, params)[source]¶

Impedance of a general capacitor

Here used for the shunt capacitor (coupler) at the start of the TL

Parameters

omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

shunt capacitor impedance

Return type

complex

stlabutils.TLmodel.Zincircuit(omega, params)[source]¶

Analytical dalculation of input impedance of a TL resonator with a shunt capacitor

Is only valid for a shunt coupler and depends on the definition of Zload(). Zload() is the impedance of the load on the far end of the TL resonator (opposite the coupler). Examples can be an open/short/junction end of the transmission line resonator. This is an analytical calculation using transmission line formulas (from Pozar). There are no lumped element approximations or equivalents involved.

Parameters

omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

Zin – Impedance seen at the resonator input

Return type

complex or array of complex

stlabutils.TLmodel.Zincircuit_approx(omega, params)[source]¶

Lumped equivalent calculation of input impedance of a TL resonator with a shunt capacitor

Is only valid for a shunt coupler and assumes the load impedance is params['Lg']. This is a lumped equivalent calculation of the TL resonator with either an open or a short end.

Parameters

omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

Zin – Impedance seen at the resonator input

Return type

complex or array of complex

stlabutils.TLmodel.Zload(omega, params)[source]¶

Impedance of a load at the far end of the TL resonator

Currently includes the possiblitity for an RCSJ and a capacitor as load

Parameters

omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

Z – load impedance

Return type

complex

stlabutils.TLmodel.Zparallel(*args)[source]¶

Parallel impedance of a collection of impedances

Parameters: *args (complex) – Values of impedances to be put in parallel
Returns: result – parallel impedance
Return type: complex

stlabutils.TLmodel.Zx(x, omega, params)[source]¶

Impedance at a given distance along the TL

Distance x counts from the load (at 0) to l (at input)

Parameters

x (float) – Position along the TL to calculate the impedance at, counting from the load (at 0) to l (at input)
omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

result – Impedance at a given distance along the TL

Return type

complex

stlabutils.TLmodel.alpha(omega, params)[source]¶

Attenuation constant of a TL

Parameters

omega (float or array of float) – Angular frequency
params (dict) – Dictionary containing model parameters

Returns

Attenuation constant given in the parameters

Return type

float

stlabutils.TLmodel.f0(params, ffs=None)[source]¶

Finds the approximate resonance frequency in Hz from a generic circuit impedance

This is an approximation which can then be used to a fitting function as starting value

Parameters

params (dict) – Dictionary containing model parameters
ffs (None or array, optional) – Frequency range in Hz to evaluate the circuit impedance at. By default 2-10 GHz

Returns

wres – Approximate resonance frequency in Hz

Return type

float

stlabutils.TLmodel.omega0(params, wws=None)[source]¶

Finds the approximate angular resonance frequency from a generic circuit impedance

This is an approximation which can then be used to a fitting function as starting value

Parameters

params (dict) – Dictionary containing model parameters
wws (None or array, optional) – Angular frequency range to evaluate the circuit impedance at. By default 2-10 GHz * 2pi

Returns

wres – Approximate angular resonance frequency

Return type

float

Table of Contents

Previous topic

Next topic

This Page

TLmodel – Model for transmission line resonator¶

Functions¶